Wisp Unification Theory - 7 Wisp & Special Relativity: Fundamentals
- Home
- About Me
- Reasons why Einstein was wrong
- One-way speed of light experiments
- Hot topic
- Q&A
- ACES - The end of Relativity

- Book Contents
- Introduction
- 1 Matter,Space and Time
- 2 Symmetry
- 3 Fractals
- 4 Wisp Space
- 5 Gravity
- 6 Electromagnetic Force
- 7 Wisp & S.R: Fundamentals
- 8 Wisp & S.R: Electrodynamics
- 9 Wisp & S.R: Doppler effect
- 10 Wisp & S.R: Relativistic Mechanics
- 11 Big bang
- Appendix A
- Appendix B
- Index A-Z
- Copyright
- Feedback
This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.
7
Wisp and Special Relativity: Fundamentals
In 1905 Albert Einstein published his special theory of relativity while
working in a Swiss Patent Office in Berne. The theory is world-class and
has influenced scientific thinking more than any other theory in history.
He used the word ‘special’ to relate to uniform motion in a
straight line.
Einstein knew that there was a need for a new theory that could explain
the relationship between measurements made in different reference frames
for Maxwell’s electromagnetic laws, as Newtonian mechanics could
not adequately do this.
Einstein solved the problem by joining space and time together, and by
using Hendrik Lorentz’s coordinate transformations. His remarkable
understanding of the nature of time lead to the development of time dilation
– time runs slower for moving observers, even though they are unaware
of it.
Now, nearly 100 years on, special relativity still remains a powerful
mathematical tool. Tests still show its predictions to be correct and
it remains a remarkably successful theory. But the theory gives no real
answers as to why physical processes behave the way they do, whereas wisp
theory does provide answers.
The famous null result of the Michelson–Morley ‘ether’
experiment secured credibility for Einstein’s new concepts of space
and time, but wisp theory can explain this result and the physical processes
behind it.
Wisp theory does not agree with special relativity’s claim that the
speed of light stays constant for all observers in motion, although plenty
of evidence seems to suggest it does. It challenges both postulates of
special relativity, but supports its concept of time dilation. It treats
space and time as being separate, and uses the notion of absolute reference
frames in which wisps are at rest. Only when observers move through absolute
frames do they experience dilation effects.
Wisp theory offers explanations for: the cause of time dilation, mass
increase in high-speed subatomic particles, and the Lorentz force law
for moving charges.
Special relativity is a simple theory that was developed from simple,
clearly defined postulates – even though they appear to defy our
common sense notions of space and time. Wisp relativity, too, develops
from simple principles, which incorporate: Newtonian mechanics, a type
of Galilean relativity, and Einstein’s time dilation for moving observers.
First we look at Einstein’s two postulates
of special relativity, and consider what implications arise from them.

Albert Einstein © Kim Albinson
7.1 Postulates and implications of special relativity
7.1.1 Postulate 1: principle of relativity
All laws of physics have the same mathematical form in all reference frames
moving at constant velocity.
7.1.2 Postulate 2: absoluteness of the speed of light
The speed of light in a vacuum has the same measured value in all reference
frames moving at a constant velocity.
7.1.3 Implications of postulate 1
This postulate expresses the absence of a universal reference frame. It
implies that there is no deviation of any laws of physics in a ‘vehicle’
travelling at any constant speed in a straight line.
It uses the Lorentz coordinate transformations for this purpose, but this
requires that we make changes to our common sense notions of space and
time:
- Observers in relative motion do not agree on the times and
places of separated events. - They observe each other’s lengths to contract in their
directions of motion. - They each record the other’s time as running slow.
Experimental evidence for special relativity’s predictions seems
overwhelming. But when we look for direct proof we find that there is
no direct evidence, i.e. no observers have travelled at high-speeds and
carried out experiments to see if the laws of physics remain the same.
It is true that fast-moving clocks run slow and fast-moving subatomic
particles seem to gain mass. But this does not provide direct evidence
to support this postulate.
The experiments that have been carried out on the Earth and aboard satellites
are one-sided: the thing being tested moves and is subjected to relativistic
effects, while the observers remain practically stationary and experience
no relativistic effects. So we cannot truthfully claim that this postulate
is correct. Wisp theory will prove that it is incorrect.
In wisp theory, if we set an observer’s speed through wisp space
to zero, then all of its relativistic equations reduce to those found
in special relativity.
7.1.4 Implications of postulate 2
Over the years, experimenters have measured the speed of light with greater
and greater accuracy. Today, it is taken for granted that its speed is
known exactly, and very few experimenters question this. However, wisp
theory shows that these experiments are flawed, because the light always
travels in two or more directions – reflected by mirrors.
To measure the speed of light correctly, measurements must be made in
one direction only (no mirrors).
No one has accurately measured the speed of light one-way on the surface
of the Earth! Wisp theory predicts that if this were to happen, its speed
would be found to vary – depending on the motion of the Earth through
wisp space. Wisp space is a type of ether medium that limits the speed
of light to an exact value.
Many experiments have been carried out to measure the speed of the Earth
through the ether. The most famous was the Michelson–Morley experiment
in 1887. But it produced the famous null result, casting doubt on the
existence of the ether and forming an experimental base for the idea stated
in this postulate.
7.2 The principles of wisp relativity
Wisp theory develops using concepts based on common sense notions of space
and time, and so avoids the paradoxes found in special relativity. It
is a type of ether theory, which predicts the null result of the Michelson–Morley
experiment, and all the observable predictions of special relativity for
Earth-based observers.
The principles of wisp relativity are as follows:
7.2.1 Principle 1 Laws are different
The laws of physics are different in inertial reference frames moving
at speed relative to stationary wisp space.
7.2.2 Principle 2 Absolute speeds are constant
The speeds of light and transverse force through one-state space are equal
and constant when measured by an observer at rest in wisp space, and are
unaffected by their sources’ motions.
7.2.3 Principle 3 Dilation factor
The dilation factor gamma is equal to the speed of light c, divided by
an observer’s absolute relative transverse light speed vt.
That is gamma is
![]()
7.2.4 Principle 4 Jiggle dilation
Bodies of matter agitate or jiggle wisp space as they pass through it.
Jiggle is the sum effect of motions caused by quantum waves passing points
in wisp space. Its effect dilates specific properties of matter by the
factor gamma. It reduces the speed of light and transverse force by gamma
in directions at right angles to a body’s motion through wisp space.
7.2.5 Principle 5 Force and time dilations
In inertial reference frames moving through wisp space, light-pulse clock’s
time (without jiggle dilation) is slowed by gamma. The speed of transverse
force is reduced by gamma. Mechanical and biological clock’s time
(including atomic) is slowed by gamma (includes the jiggle dilation effect).
Consequently moving observers must apply the rules for time dilation compensation
(Section 7.15.4) to all physical processes that take place in their reference
frames.
7.3 Measurements: absolute and relative
We briefly discussed these measurements here and follow up later with
more detail.
7.3.1 Absolute measurements
Absolute measurements are those made in reference frames that are stationary
with respect to one-state space. Time in these frames is absolute and
unaffected by time dilation.
If we place identically prepared clocks throughout stationary one-state
space, they will all remain synchronized and record the same absolute
time.
7.3.2 Relative measurements
Relative measurements are those made in reference frames that move through
‘stationary’ wisp space. Clocks placed in these frames would
record relative time and run slower than ‘stationary’ absolute
clocks, because of the effect of time dilation.
In equations, I show variables primed when they apply to measurements
made by observers moving through wisp space, for example:
- t is absolute time measured by observers who are stationary in wisp space.
- t’ is relative time measured by observers who are moving through wisp space.
When we move through wisp space, time dilation slows down our bodies’
senses (body clocks), causing us to become unaware of its effects. Consequently,
we observe all physical processes to appear to take place at normal speeds
within our frames. However, what we are observing are the effects of an
illusion. If we could see processes taking place within slower frames,
they would appear to take place speeded up.
Since our senses automatically compensate for time dilation, we must apply
the rules for time dilation compensation (Section 7.15.4) to all physical
processes that take place within our frames. (Square brackets [ ] are
used to identify time dilation compensation terms within equations.)
If, when we move through wisp space, we were to modify our body clocks
to work only in absolute time, we would see things happen in slow motion
within our frames, but would see things happen at normal speeds in ‘stationary’
absolute frames.
7.4 Events
An event is an occurrence, which happens at a definite location and time
in wisp space.
In wisp theory absolute simultaneity of events is not lost. If observers
could record events using absolute clocks, they would all agree on the
absolute times and locations of events in wisp space.
But observers who move through wisp space record relative time –
due to the effect of time dilation – and so may not agree on the
timing of events.
In special relativity all motions are relative (there is no absolute frame)
and observers in relative motion will not agree with each others’
times or locations for separated events. This loss of simultaneity defies
common sense, and many scientists including Lorentz found this too difficult
to accept. But Einstein did not, and he developed new ideas for space–time
in which an observer’s relative motion affects the very fabric of
space–time itself.
7.5 Absolute measurements of light’s relative speed
We start by determining the relative speed of light in different reference
frames. The speed of light c through absolute one-state space is constant
when measured in absolute space and time.
Current measurements indicate that the relative speed of light in a vacuum
is always constant, regardless of an observer’s motion – special
relativity’s postulate 2, but wisp relativity’s principle 2,
states that it is not constant. Wisp theory will show that the speed of
light gets recorded using current methods as being constant, while at
the same time its relative speed varies, so do not be concerned with this.
7.5.1 Absolute measurements in a stationary frame
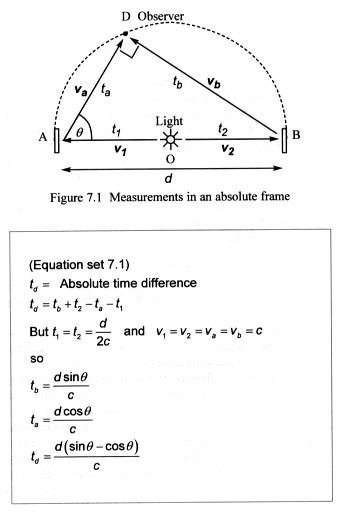
We first calculate the absolute time difference taken by light to travel
along separate paths to an observer at D (Figure 7.1). (Many light speed
experiments look for a time difference to determine whether or not the
speed of light stays constant.)
A light source O is placed centrally between two mirrors A and B. The
mirrors lie across the diameter d of a semicircle, and the observer
D moves freely on its arc. The apparatus remains stationary in one-state
space.
We switch on the light source and record the absolute time difference
td (Equation set 7.1). All measurements
are absolute, since the apparatus is stationary in wisp space.
With angle theta= pi/4 radians, D is central, and td
= 0. This shows that the times taken for the two light rays to travel
to a centrally placed observer are equal.
7.5.2 Absolute measurements in a moving frame
We repeat the measurements with the apparatus moving through wisp space
at speed V (Figure 7.2).
Measurements are taken from absolute clocks fixed throughout wisp space,
which record the times when the moving apparatus passes fixed points (relative
time is ignored).
Light emits from a fixed point in wisp space (Wisp relativity’s principle
2). As the light travels along its separate paths, the apparatus moves
through wisp space, and the origin of the semicircle O moves away from
the light’s point of emission. Equation set 7.2 gives the absolute
values for times t1 and t2.
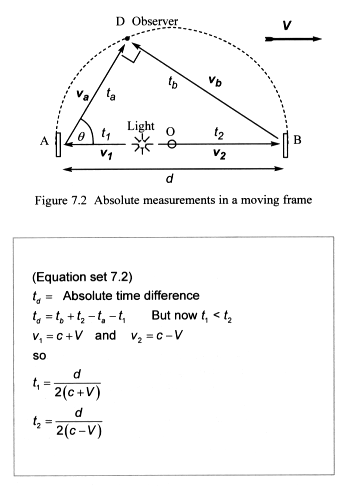
A stationary observer in wisp space sees the light strike
mirror A first, because the mirror is moving towards light’s fixed
emission point. And the light takes longer to reach mirror B, which is
moving away from the emission point.
Before we calculate absolute values for ta and tb we need to determine
the absolute measurements of light’s relative speed in all directions
in the moving frame.
Imagine that you are the observer D moving at speed V through wisp
space and your senses have been specially modified to work in absolute
time, so that the time dilation effect is absent. You would measure the
relative speed of light reflected from the moving mirror to vary depending
on the angle theta and speed V.
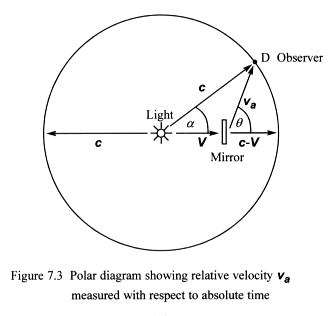
Figure 7.3 shows the relative velocity of light va
reflected off the moving mirror – as measured with absolute time.
The relative speeds of light clearly differ from speed c, but do not be
concerned with this.
We need to find an expression that shows va in terms of V, c and
angle theta. Equation set 7.3 gives the formula.
Now, referring back to Figure 7.2, ADB is a right-angled triangle and
so distance AD = d cos (theta).
Now we just need to find ta, and
ta = AD / va measured in absolute time.
Similarly vb (relative speed of light travelling from B to D, Figure 7.2) is found by substituting the angle (pi/2 + theta ) and calculating the positive root (Equation set 7.4). This yields a larger value than va because the light has a component of its velocity in the opposite direction to V.

Figure 7.4 and Equation set 7.3 shows more detail and the maths used to
calculate the relative velocity of light.
We have now produced equations that enable us to calculate absolute time
intervals for light’s journey in fixed and moving frames. But before
we consider how these times relate to an observer placed in a moving frame,
we need to consider the effect of Einstein’s time dilation.

7.6 Dilation factors
7.6.1 Time dilation: light-pulse clocks
Time is an abstract notion and as such does not exist as a physical substance,
but we can use physical systems to measure its flow.
Einstein used a hypothetical ‘light-pulse clock’ to measure
time in special relativity. He predicted the time dilation effect from
studying the periodic motion of a pulse of light bouncing between two
mirrors.
Time dilation is an expansion of the time interval measurement between
ticks in a moving clock, which causes time in moving clocks to run slow.
Wisp relativity’s principle 3 states: The dilation factor gamma is
equal to the speed of light c, divided by an observer’s absolute
relative transverse light speed vt. That
is gamma is
![]()
Our bodies are mechanical and so are affected by time dilation in the
same way as moving mechanical clocks are. The mechanical time dilation
effect on Earth just happens to be the same as Einstein’s light-pulse
clock. Everything (except longitudinal force) has its time slowed down
by gamma. Our senses, however, are unaware of the effect – passing
of time appears normal to us.

Equation set 7.5 shows the general dilation equation. The important
point to understand is the way matter-fractals move through wisp space:
Their movements displace surrounding wisps at right angles to their directions
of motion, and only their fractal shapes travel in their directions of
motion through wisp space.
So the dilation effect experienced by all types of moving matter (including
mechanical and atomic clocks) is due solely to right-angle motions, where
angle theta = pi/2 radians.
Substituting this value into the general dilation equation gives the dilation
factor gamma, which just happens to be the same formula as that used by
Einstein for time dilation in moving clocks. Although Einstein derived
time dilation using a different method and based on different principles,
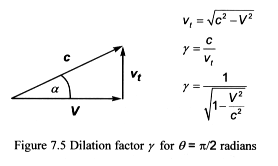
the effect is the same.
Figure 7.5 shows a simple vector diagram used to calculate the dilation
factor for matter moving through wisp space – due solely to right-angled
motions of wisps. The relative transverse velocity of light is given as
vt.
The time dilation effect measured on the Earth for high-speed subatomic
particles is always that given by Einstein’s formula (identical to
wisp’s formula for theta = pi/2).
An observer who travels in a craft moving at near light speed would be
affected by Einstein’s time dilation, but would also notice that
the relative speed of light varied throughout the craft, creating illusion
effects – see front cover image. This is because the relative speed
of light is dependent upon the angle theta it makes with the craft’s
velocity V.
7.6.2 Force dilation
Transverse force propagates at the speed of light and so is dilated by
the factor gamma. The force’s substance does not diminish, only its
effect near light speed diminishes.
Force dilation is one of two factors that slow time in moving mechanical
clocks – the other factor is jiggle.
Force and jiggle dilations also affect moving gravitational and electromagnetic
forces.
7.6.3 Jiggle dilation
When matter-fractals move through wisp space, their zero-state spheres
push wisp space apart, creating quantum waves patterns. These are transverse
waves that cause wisps to oscillate in directions at right angles to the
matter-fractals’ directions of motion. At any point in wisp space
the agitation or jiggle is the sum effect of all transverse waves passing
that point. This produces random motions at points in wisp space and causes
dilation of the transverse force by the factor gamma.
Around any large body moving through wisp space the jiggle motions can
be grouped into planes that are at right angles to the body’s motion
(Figure 7.6).
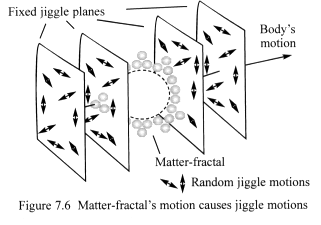
Jiggle has the effect of reducing the strength of the electric charge
on a body moving through jiggle planes. This is equivalent to an effective
increase in the value of the electric constant or absolute permittivity
of free space – by gamma.
Similarly the magnetic constant or permeability of free space – increases
by gamma.
The magnetic and electric fields of light move at right angles to its
direction of motion. When light travels parallel to jiggle planes, one
or both of these fields experience random fluctuations as they transverse
through adjacent jiggle planes. This has a net effect of reducing the
speed of light by gamma (this is the cause of the famous null result of
the Michelson–Morley experiment).
Light travelling at right angles to jiggle planes has magnetic and electric
fields that move within the planes, and so jiggle motions are equally
added and subtracted, producing no net change in the speed of light.
Charged particles that move through jiggle planes will experience a reduction
in the strength of their electric charge in all directions of motion:
- Charged particles that travel parallel to jiggle planes displace their electric fields at right angles to their directions of motion. Their charge crosses into adjacent jiggle planes, which reduces its strength by the jiggle dilation factor gamma.
- Charged particles that travel at right angles to jiggle planes displace their electric fields within the planes. But the motions of the particles transfer the shape and structure of their electric fields across neighbouring jiggle planes, and so the jiggle motion effect is induced, again reducing the strength of the charge by the jiggle dilation factor gamma.
It is the motions of matter-fractals’ zero-states spheres through
wisp space that are responsible for creating jiggle motions. Since light
is an electromagnetic wave, it does not possess a zero-state sphere, and
so does not create jiggle motions.
Likewise forces propagate through wisp space without creating jiggle motions.
7.6.4 Time dilation: mechanical/biological clocks
Everything made from matter associates with mechanical clocks for measuring
the passing of time – absolute or relative time.
A mechanical clock’s internal components move at speeds much less
that that of light, and so we can use classical equations to calculate
its internal forces.
The rule for time flow in all material bodies is:
- The strength of the transverse force operating within these bodies determines the rate at which time flows.
In simple harmonic motion devices such as pendulums and masses on oscillating
springs, periodic time intervals vary inversely proportional to the square
root of the force – gravitational or spring respectively.
Bodies that move through jiggle planes are affected by both transverse
force dilation and jiggle dilation, which has the net effect of reducing
the strength of the forces within the bodies by gamma squared.
Equation set 7.6 gives an example that shows the time dilation effect
in a simple mechanical clock.
The period of oscillation for simple harmonic devices therefore increases
by gamma. This just happens to produce the same time dilation effect that
Einstein discovered.

Time dilation causes all physical processes that happen in moving frames
to slow down. However, moving observers are unaware of its effects as
their senses are automatically compensated – see section 7.15.4 (Rules
for time dilation compensation).
We now know that a physical process – force and jiggle dilations
– causes time dilation, and that it is not an inherent property of
time itself that results from Einstein’s concept of space–time.
7.7 The Michelson–Morley experiment
Of the experiments designed to measure the speed of the Earth through
the supposed luminiferous ether, the most famous was that performed by
Michelson and Morley in 1887.
The Michelson interferometer (Figure 7.7) is mounted on a horizontal turntable
so that it can be rotated relative to the motion of the ether stream.
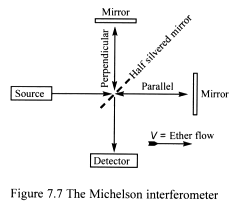
Monochromatic (one wavelength) light is directed at a half-silvered mirror,
which splits it into two beams. These travel in different directions,
along and across the ether stream, and then recombine to interfere either
constructively or destructively, producing a pattern of light and dark
fringes.
According to classical physics, light should take different times to travel
along the paths, and the time difference should show up as a shift in
the observed interference pattern.
Even though the experiment was carried out with great accuracy, and repeated
with the apparatus rotated through 90°, the results were always the
same – zero.
Possible explanations for this result are either that the Earth’s
motion through the ether cannot be detected by this method or that the
supposed ether does not exist.
George Stokes provided a theory on ether drag as a possible solution.
It predicted that null result would occur because somehow the Earth dragged
the ether along with it.
Wisp theory does not support this notion, because wisps have mass, and
the effect of dragging wisp space would increase the Earth’s mass
enormously. So we can clearly rule out this possibility.
Wisp theory holds the view that the Earth moves effortlessly through wisp
space, because it is made of matter-fractals that are part of wisp space.
The motion of the Earth (a large body of matter-fractals) through wisp
space creates jiggle plane motions. This causes jiggle dilation, which
reduces the speed of light in directions at right angles to the Earth’s
direction of motion.
The Michelson interferometer fails to measure the Earth’s motion
through wisp space because the effect of jiggle dilation cancels out the
expected small time difference for light to travel along opposite paths.
Equation set 7.7 shows the equations for the experiment, which include
the jiggle dilation effect. Jiggle dilation produces a zero result for
all wisp space (ether) speeds.
It should also be noted that because of the effects of time and jiggle
dilation on the Earth’s surface, light’s measured speed is relative
– see section 7.16 (Absolute speed of light).

7.7.1 One-way light speed test
Modern methods that calculate the speed of light by measuring its time
along two or more paths are fundamentally flawed.
In the case of the Michelson–Morley experiment, the gain and loss
in light’s speed along the parallel arm exactly match that for the
speed in the perpendicular arm, due to the jiggle
dilation effect. So scientist have wrongly assumed that the speed
of light is constant in all directions.
Only by making accurate measurements along a single path (no mirrors)
can the true relative speed of light on the Earth’s surface be determined.
But the motion of the Earth through wisp space and the effects of time
and jiggle dilation need to be taken into account before the absolute
speed of light can be determined – see section 7.16 (Absolute speed
of light).
A test to measure the speed of light one-way is as follows:
Two receiver/transmitter stations are placed on the equator a large distance
apart, each contains a high-precision atomic clock and high-power laser.
At the moment the stations line up perpendicular to the Earth’s orbit,
their clocks synchronize by sending pulses of light to each other. Synchronization
is possible because the relative speeds of light in perpendicular directions
are equal.
Six hours later the stations will be parallel to the Earth’s orbit,
and each station can independently fire a pulse of light to the other,
and separately measure the time light takes to travel one-way.
Wisp theory predicts that the motion of the Earth through wisp space affects
the relative speed of light. By comparing one-way journey times, a non-zero
difference will result. The difference in time recorded for journeys with
and against the wisp space flow is L × 6.67×10^-13 seconds,
where L is the distance separating the stations.
7.8 Kennedy-Thorndike experiment
In 1932, Roy Kennedy and Richard Thorndike performed a modified Michelson–Morley
experiment, in which the lengths of the light paths were different.
The purpose of the experiment was to check the viability of the Lorentz-FitzGerald
contraction proposal – a body moving through the ether contracts
by gamma in its direction of motion.
Tests carried out over several months found no evidence of contraction
effects and the results were unaffected by the Earth's motion rotating
the apparatus.
The length contraction proposed by special relativity applies to moving
observer reference frames and not the frame in which the test apparatus
resides.
Both wisp theory and special relativity predict equal values.
7.9 Stellar aberration
In 1725 James Bradley discovered stellar aberration: a yearly variation
in the angular displacement of the position of stars. A combination of
the motion of the Earth in its orbit and the speed of light cause this
effect.
In 1728 Bradley measured the angular displacement a, and from it calculated
the speed of light to within 5 per cent.
The angle a is approximately 20 arc seconds and is calculated using alpha
= arctan V/c, where V is the speed of the Earth orbiting
the Sun and c is the speed of light (Figure 7.8).
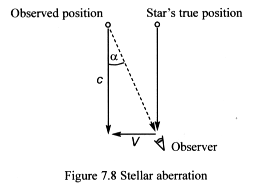
Early ether theories proposed that the speed of the ether relative to
the Earth would affect the direction of light striking it. If the ether
was dragged along by the Earth, the approaching light would be carried
along with it and remain at the same approach angle and the aberration
would be zero.
Wisp theory predicts that the speed of wisp space (ether) relative to
the Earth will not change the direction light takes. If during its long
journey, the light from the star passes through moving one-state space,
its speed will alter slightly but not its direction.
The aberration angle is simply an optical effect that results from the
addition of velocities. Both special relativity and wisp theory predict
similar results.
7.10 Fizeau’s experiment
In 1851 Armand Fizeau performed an experiment to measure the speed of
light in moving water. The purpose of the experiment was to measure the
value of the ether drag coefficient predicted earlier by Augustin Fresnel.
Both Fresnel and Einstein developed theories that correctly predicted
the speed of light in moving water. Wisp theory uses their equations,
but modifies them to conform to wisp theory’s principles.
The results (shown in Appendix B) suggest that the Earth’s motion
through wisp space cause a small, but constant offset, which increases
previously predicted results by a factor of 1.000265.
Using sensitive measuring equipment it may be possible to detect this.
7.11 Wisp coordinate and frame velocity transformations
These allow us to take positions and times measured in one frame, S, and
transform them to positions and times measured in another frame, S’.
In wisp theory, space and time are absolute, and so we use a variation
of the transformations of classical physics developed by Galileo Galilei
and Isaac Newton as a starting basis. However, we know that the effect
of time dilation on particles moving through wisp space is real, so we
must include Einstein’s time dilation in moving frames.
Consider an event E1 occurring at some point
in space and time (Figure 7.9). To an observer placed at the origin of
frame S – stationary in wisp space – the coordinates of the
event are x1, y1, z1,
t1.
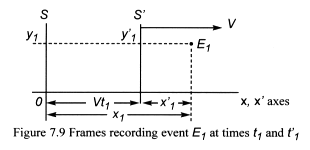
A second observer is placed at the origin of moving frame S’, which
moves through wisp space at speed V in the direction of the x-axis. The
axes of their frames remain parallel, and at time t = 0, both observers
set their clocks to zero. The observer in frame S’ records the event
as x’1, y’1, z’1,
t’1.
The measurements in stationary frame S are with respect to absolute space
and time, while those in the moving frame S’ include the time dilation
effect. Both observers will agree on the location within wisp space of
the event, but they will not agree on the time at which the event occurred
– unless the event occurred at t = 0.
Equation set 7.8 shows the wisp coordinate and frame transformations.

7.11.1 Wisp frame velocity transformation
A moving observer’s time runs slow because of the effect of time
dilation, and stationary observers are seen to approach or recede at faster
speeds because of this.
Time has not changed for stationary observers; they see things according
to Galilean relativity where time and space remain absolute.
An observer moving through wisp space at light speed divided by ‘the
square root of two’, would see stationary observers approach or recede
at the speed of light. If a moving observer’s speed through wisp
space were greater than this, they would see stationary observers approach
or recede at speeds greater than light.
Of course light does not travel faster than speed c through wisp space,
but the effect of time dilation on moving observers creates an optical
illusion that it does.
7.12 Invariance of distance
Space is absolute and so all observers whether stationary or moving must
agree on distance measurements between points in wisp space.
Wisp theory does not use the notion that moving objects shorten their
lengths in their directions of motion relative to stationary observers
– known as the Lorentz-FitzGerald contraction.
All observers in wisp space record the same locations and absolute times
for events.
Observers in motion through wisp space will experience the time dilation
effect and will unknowingly record measurements in relative time. By using
wisp transformations we can convert relative measurements to absolute
measurements.
7.13 Absolute simultaneity: events
In a stationary frame S a ball rolls across a table, which is 1 m wide,
and the table moves at speed V along the positive x-axis (Figure
7.10).
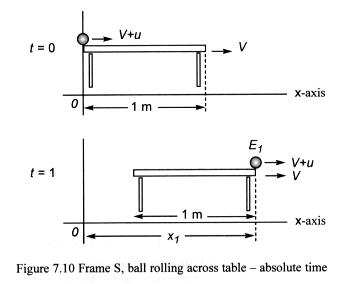
At time t = 0, the ball is at the origin of the x-axis (we can think of
this as event E0) and it rolls across the
surface of the table at relative speed u in the positive x-axis
direction. The absolute speed of the ball is V+u. Let u = 1 m/s
and V = 0.6c. After 1 second of absolute time, the ball reaches
the end of the table and the event is recorded in absolute measurements
as E1, where
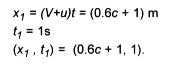
An observer moving with the table in frame S’ (Figure 7.11) will be affected by time dilation, and consequently will record an increase in the speed at which the ball moves across the table.
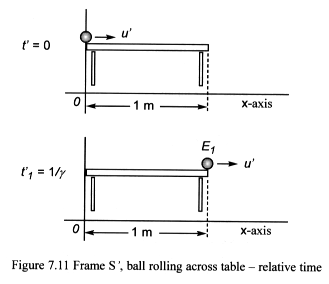
The ball travels faster by the factor gamma, when measured using relative
time. However, this relative speed increase is an illusion caused by time
dilation, and all absolute measurements are unaffected.
The relative time t’1 taken for the ball to
move across the table is therefore shorter than the absolute time by the
factor gamma. However, the event is recorded as occurring at the same
point in space and time when recorded by absolute clocks fixed throughout
wisp space.
The event calculates to the same values as before
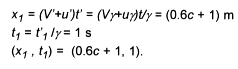
According to both stationary and moving observers, the events (E0
and E1) take place at the same points in
wisp space and at the same absolute times. So wisp theory supports the
concept of absolute simultaneity, whereas special relativity does not.
The effect of time dilation slows time for the moving observer who witnesses
the event after a shorter period of relative time 1gamma’ or 1/gamma
seconds.
Of course being able to detect the motion of wisp space in the first place
is essential to establishing a reference to absolute time, and hence be
able to determine if the effect of time dilation applies to a particular
frame.
Light speed measuring devices capable of measuring speeds one-way will
make determining the motion through wisp space commonplace in the near
future.
7.14 Mass invariance
In wisp theory, a particle does not gain mass as it speeds up, but it
does increase its kinetic energy.
The supposed mass increase of subatomic particles moving at speeds close
to light is in fact a quasi-mass increase caused by the effect of transverse
force dilation.
Einstein’s mass energy equivalence equation E = mc^2 suggests
that energy and mass are interchangeable, and this is well proven. This
does not result from a particle’s mass increasing with speed, but
is related to a process whereby particles’ zero-state spheres join,
expand or shrink during collisions – see section 10.2.1 (Energy into
mass).
7.14.1 Relativistic mass increase: quasi-mass
It is a known fact that subatomic particles’ masses appear to increase
as they approach the speed of light.
The standard equation for mass increase is

Where m’ is the mass of the particle moving at relative speed
V, mo is its rest mass, and c is the speed of light.
However, the numbers of wisps that make up a moving particle’s matter-fractals
have not increased, and so its real mass stays the same. The only possible
explanation for the perceived mass increase is for the force acting on
the particle to reduce in strength, because transverse force travels at
the speed of light, and consequently it is not possible to accelerate
a particle faster than that speed through wisp space.
As the speed of light is approached, the effect of the transverse force
drop to zero, giving the impression that the particle’s mass has
increased. But in reality it has not, its mass stays the same. So we say
that mass is invariant or
m’ = m.
We conclude, that the perceived mass increase (quasi-mass) experienced by fast moving particles is due to the effect of the forces acting on it being reduced by the dilation factor gamma.
7.14.2 Accelerating subatomic particles
A particle accelerator in a laboratory accelerates electrons (Figure 7.12).
Force-devices in the laboratory generate powerful magnetic and electric
forces that act on the electrons, accelerating them along circular paths
to near the speed of light.

The force-devices remain stationary with respect to the laboratory’s
frame and so stay fixed within the laboratory’s perpendicular jiggle
planes. So jiggle dilation does not affect the forces generated in the
laboratory – since positive and negative jiggle motions cancel out
within the jiggle planes.
The figure shows the electric force lines Fe
grouped into columns within the jiggle planes. For clarity, magnetic field
lines are not shown, but they too would lie within the planes.
The laboratory’s forces are unaffected by jiggle motions, but their
effects are depleted near the speed of light, due to the effect of transverse
force dilation. And so the electrons cannot accelerate past the speed
of light. The quasi-mass effect is created as the electrons speed up,
but in reality it is the force acting on them that diminishes.
The other effects of importance are the dilations within the moving electrons.
Here transverse force dilation occurs, because the electrons are moving
at high-speed through wisp space. But also, because they move through
the laboratory’s perpendicular jiggle planes, they experience the
effect of jiggle dilation. As a consequence, the internal forces Fi
within the moving electrons are reduced by gamma squared, which cause
their mechanical clocks to run slower by gamma – see section 7.6.4
(Time dilation – mechanical/biological clocks).
7.14.3 Decelerating subatomic particles
If the electric force-device that had previously accelerated the electrons
to near the speed of light were suddenly reversed, the energy needed to
slow the electrons down would be exactly the same as that used to speed
them up.
A ‘reverse’ force dilation process applies, which reduces the
effect of the retarding force on particles moving at speeds close to the
speed of light. The particles behave as though they have more mass (quasi-mass)
and are harder to slow down, but this is not so.
7.15 Wisp accelerations and transformations
We examine the effects of acceleration in four ways.
- Find the magnitudes of the relativistic forces that act on a charged particle accelerating in a circular particle accelerator.
- Derive the acceleration transformations from the wisp coordinate and frame velocity transformations (Section 7.11) given earlier for a particle accelerating from rest through stationary wisp space.
- Calculate – using classical dynamics – the absolute accelerations of a particle placed in a force-device, which is first stationary, and then moving. We take into account mass invariance, and the effects of force and jiggle dilations.
- Examine the affect time dilation has on moving observers’ perspectives for physical processes that take place in their local reference frames. We must apply the rules for time dilation compensation (Section 7.15.4) to these local processes to compensate for the effect that time dilation has on local observers.
7.15.1 Particle accelerator force magnitudes
Figure 7.12 shows a strong electric field accelerating charged particles
in directions parallel to their motions. For simplicity the accelerator
is at rest in wisp space.
The rate of change of a particle’s relativistic momentum with respect
to time is a measure of the effect that a force has on it. Equation set
7.9 shows wisp’s interpretation of the standard equation for relativistic
momentum.

Equation set 7.10 shows the calculations for determining the magnitudes
of magnetic and electric forces that act on a charged particle moving
in the stationary accelerator. Remember that in wisp theory a particle’s
mass m remains constant, while the effect of the force on it diminishes
near the speed of light.

Figure 7.13 shows the effects that the two orthogonal forces (parallel
and perpendicular) have on a charged particle. The magnetic force causes
it to accelerate by changing its direction of motion, causing it to follow
a circular path (it plays no part in changing its speed) whereas the electric
force alters its speed but not its direction.

The results confirm experimental finding that for equal measures of acceleration
on a particle travelling near the speed of light, it takes a greater force
to accelerate it in a linear direction than it does to keep it on a circular
path.
7.15.2 Wisp acceleration transformations
Transformations couple measurements made in one reference frame to those
in another. By using them it is possible to predict what observers in
different frames will measure.
We compare a stationary observer’s measurements made in absolute
space and time (frame S) to a moving observer’s relative measurements
(frame S’). (We do not apply the rules for time dilation compensation
(Section 7.15.4) to transformation equations, because the equations
couple events that are non-local.)
A force-device at rest in absolute frame S accelerates a particle in the
+ x direction with acceleration a. At time t = 0 the particle is at rest
at the origin, and so its initial speed is zero, uo
= 0.
A second observer moves at speed V along the + x direction (frame
S’). Time measurements in both frames start at the moment their origins
coincide.
The acceleration transformations are given in Equation set 7.11 and they
show that a’ = a(gamma)^ 2. In other words a moving observer
sees an accelerating body in frame S accelerate at a faster rate by a
factor of gamma squared.

The effect of time dilation in a moving frame S’ creates the illusion
of increased acceleration for a body accelerating in the stationary frame
S. This is because the force-device causing the acceleration operates
in the stationary frame S and is unaffected by dilation effects (its forces
remain strong).
Moving observers’ clocks run slow, but they are unaware of this because
their body clocks also slow down.
If moving observers wished to determine the absolute accelerations of
bodies, they first need to determine their own absolute speeds through
wisp space. Only then would they be able to determine true absolute values
for accelerations.
7.15.3 Motion produced by a force-device in absolute frame S
A force-device remains fixed in absolute frame S (Figure 7.14) and produces
a force F1 that acts on a small particle
of mass m.
The particle accelerates through a distance h, reaching a maximum
speed u1. (This speed is negligible when
compared to the speed of light, and so we can ignore (gamma)u1
dilation effects.)
The device is representative of a mechanical/biological clock, to which
we can synchronize our body clocks. A series of particles singularly pass
through the device, each representing one beat of our body clocks –
say one second.
We can also infer that the beat of this clock is proportional to the speed
at which our brains process information and it determines our sense of
the flow of time.
The motion of particles in the device is in accordance with classical
dynamics, and because the device is stationary in wisp space, relativistic
effects are ignored (Equation set 7.12).

7.15.3.1 Motion produced by a force-device moving in frame S
A force-device moves through absolute wisp space (frame S) at speed V,
and so is subject to the effects of force and jiggle dilations.
In frame S, a stationary observer records absolute measurements of the
motions of the particles in the moving force-device. Applying the rules
for time dilation compensation (Section 7.15.4) to the stationary
observer has no effect on the absolute measurements recorded.
The observer notices that the time the particles spend in the moving force-device
is now longer than if it were stationary. This is because the effects
of force and jiggle dilations physically reduce the effectiveness of forces
that operate within the device, causing the particles to accelerate more
slowly.
The relative motion of the particle to the force-device is u2,
which is negligible when compared with the speed of light, and so we can
ignore additional relativistic effects. However, the speed at which the
force-device moves through wisp space could be significant and so we must
take into account the effects of force and jiggle dilations acting on
the force-device. They reduce the strength of the force F2
operating within the device, so the classical dynamics equations used
earlier need modifying accordingly (Equation set 7.13). All measurements
are absolute.

If the moving force-device slows its beat by a factor of two, then for
two beats of an absolute clock, the moving clock would beat once when
measured in absolute time.
Now if we substitute our bodies in place of the force-device, our body
clocks would run at half speed in absolute time. But we would be unaware
of this fact, because our senses would slow down and time would appear
to run at normal speed.
Jiggle and force dilations affect all physical processes that take place
on the Earth as it moves through wisp space. But our senses automatically
compensate for the effects of time dilation (caused by force and jiggle
dilations), which cancels out our awareness of its slowing effect on physical
processes that surround us.
Consequently we must apply rules for time dilation compensation
(Section 7.15.4) to simulate the actions of our senses when confronted
with time dilation effects. And we will find that physical systems that
move through wisp space behave in the same way as ones that are stationary.
Before testing this out on the moving force-device we will look at the
rules for time dilation compensation.
7.15.4 Rules for time dilation compensation
Moving observers’ body clocks slow in the same manner as moving mechanical
clocks do, and so they are unaware of the effect of time dilation. Without
their knowledge the rules for time dilation compensation (Equation
set 7.14) are automatically applied, and any measurements they make are
with reference to relative time.

To compensate for observers’ time slowing, we must apply the rules
for time dilation compensation to all physical processes that are
‘local’ to their moving reference frames.
The next example will demonstrate this.
7.15.4.1 Motion produced by a moving force-device with respect to frame
S’
An observer travels with a moving force-device and is unaware of its motion
through wisp space. In the observer’s frame S’ the force-device
appears stationary.
A stationary wisp space observer in frame S sees the force-device moving
and sends the moving observer information about its absolute measurements
(Equation set 7.13). The moving observer then applies the rules for time
dilation compensation (Equation set 7.14) to the absolute measurements,
which converts them into relative ones.

Equation set 7.15 shows the compensated data. The moving observer’s
predicted measurements are shown primed. (Square brackets [ ] are used
to identify time dilation compensation terms.)
The moving observer then carries out local measurements on the motions
of particles in the force-device, and discovers that the measurements
agree with those predicted. All timings, accelerations, speeds, energy
and momentum increases are identical. Both observers find that their force-devices
operate identically in their local reference frames according to known
laws of physics.
If they were unaware of the motion of wisp space they each would wrongly
conclude that the laws of physics were the same in all inertial frames
(special relativity’s postulate 1).
Sceptical of the findings, the moving observer asks for confirmation about
the truth of the absolute measurements supplied. And both observers agree
to watch each other as they repeat their experiments.
The stationary observer in frame S sees the moving observer’s force-device
operate more slowly. And the moving observer in frame S’ – although
witnessing normal operations locally – notices that the force-device
in frame S appears to be working more quickly.
The moving observer finally accepts that time dilation, coupled with the
effects of force and jiggle dilations, is the reason why both sets of
local measurements appear identical.
7.16 Absolute speed of light
The speed of light measured on Earth in a vacuum is 299,792,458 m/s. Although
this value does not take into account the effects of time dilation caused
by the motion of the Earth through wisp space, it does give the correct
value - this measurement is based on two-way speed of light experiments.
Light's two-way speed on Earth is slowed by gamma due to a combination
of jiggle effect and c+/-V summing. However, by making two-way speed of
light measurements in relative time the slowing effect is cancelled out
by time dilation.
Equation set 7.16 shows that the true absolute value for the speed of
light is c, even though the average speed of light in two directions is
slower than this on the Earth.

7.17 Earth’s absolute and relative times
The effect of time dilation causes all clocks on the Earth to run slow
by about 762 ns each second. This happens because the clocks on the Earth
measure relative time, which runs slower than absolute time. A time interval
of 1.0 second measured on the surface of the Earth would correspond to
1.000000762 seconds in absolute time (Equation set 7.17).

Home --
About Me -- Reasons
why Einstein was wrong -- One-way
speed of light experiments -- Hot
topic --
Q&A -- ACES
- The end of Relativity --
Book Contents -- Introduction
-- 1 Matter,
Space and Time -- 2
Symmetry -- 3
Fractals -- 4 Wisp Space
-- 5 Gravity -- 6
Electromagnetic Force --
7 Wisp & S.R: Fundamentals -- 8
Wisp & S.R: Electrodynamics -- 9
Wisp & S.R: Doppler effect -- 10
Wisp & S.R: Relativistic Mechanics --
11 Big bang -- Appendix
A -- Appendix B -- Index
A-Z -- Copyright -- Feedback
