• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

9

Wisp and Special Relativity: Doppler Effect

9.1 The Doppler effect of light
The Doppler effect of light occurs when an observer moves relative to a light source, causing an increase or decrease – Doppler shift – in the frequency observed.
Special relativity appears to predict the correct Doppler effect in all cases, and this is one of its most common applications.
Scientist believe that the presence of an ether medium would cause Doppler effects that would be different to those predicted by special relativity. For example, the Doppler equations for sound and water waves – which both propagate in mediums – are completely different to those of light. So one could assume that light does not propagate in a medium, as is the case with special relativity.
However, wisp theory attributes the Doppler effect of light to motion through an absolute ether medium – wisp space, and so differs dramatically from special relativity.
The frequency predictions of wisp theory and special relativity agree almost exactly in every detail except one – a predicted increase in frequency as opposed to a decrease for a moving observer’s transverse Doppler shift.
We will examine Doppler effect case by case and make comparisons with special relativity’s predictions. And we use the results obtained to develop a single general Doppler equation for wisp theory.
We will find that if we limit an observer’s motion through absolute wisp space to zero then the equation reduces to that of special relativity’s.

9.1.1 Light source device
A stationary electronic device emits light, which travels at speed c through one-state space. It has wavelength (lambda o), and frequency fo. The period (delta T) of the electrical oscillations within the device determines the frequency of the light emitted.
When the device moves through wisp space, time dilation affects its period of oscillation, increasing it by (gamma), which in turn reduces the frequency of the light emitted.

9.2 Doppler effect

9.2.1 Doppler effect: transverse observer motion
We apply wisp’s principles to determine the Doppler effect for an observer moving at right angles to a wide stationary light source (Figure 9.1).

The wavelength of light emitted from the source has the same length in all reference frames – length invariance. And an observer measures the frequency of light by dividing its relative speed by its wavelength.
The observer is moving at right angles to light’s motion, and so no relative displacement takes place in the direction of light, and light’s relative speed (measured in absolute time) remains at c. But the moving observer experiences time dilation, and so we apply the rules for time dilation compensation (Section 7.15.4). This increases the observer’s relative speed of light by gamma, which results in an observed increase in frequency.
The value predicted for the observed relative frequency is greater than that of the source (Equation set 9.1).
Wisp theory and special relativity agree on the size of the frequency change, but disagree on its sign. Wisp theory predicts a positive value, whereas special relativity predicts a negative value.

9.2.2 Doppler effect: transverse source motion
A wide light source moves at right angles to a stationary observer (Figure 9.2).
In this case wisp theory predicts a decrease in frequency, which is the same as that predicted by special relativity (Equation set 9.2).

9.2.3 Transverse Doppler effect experiments
Experiments to measure the frequency radiated from high-speed atoms have been carried out to test for Doppler effect. The results show a decrease in observed frequency in the transverse direction, in agreement with both wisp theory and special relativity’s predictions.
In 1963 Walter Kundig carried out an experiment on transverse Doppler shift. He used a rotating turntable with a radiation source placed at its centre and an absorber placed on its rim. The relative motion of the source and absorber are transverse at all times, and so the change in frequency detected will be due solely to time dilation.
Although the results of the experiment agree with special relativity to within 1 percent, we can only say with certainty that a frequency change took place due to the effect of time dilation. We cannot say whether the change was positive or negative.
Wisp theory predicts a positive change in frequency, whereas special relativity predicts a negative change. Both predicted changes have the same magnitude and will therefore have the same effect on the absorber. The results of the experiment are therefore inconclusive.

9.2.4 Testing a moving observer’s transverse Doppler effect
A receiver placed in a polar satellite could be used to detect a small positive increase in radio frequency due to the transverse Doppler effect.
It is important that the receiver moves faster through wisp space than the frequency source. The change in frequency measured will be a few parts per billion. The satellite’s position and time measurements must be accurately recorded, as the frequency changes associated with approaching and receding Doppler effects could swamp the readings. Test instruments would need to be extremely accurate and sensitive.
Appendix A shows detailed results predicted by wisp theory, which differ slightly to those predicted by special relativity.

9.2.5 Doppler effect: observer receding from a stationary source
An observer moves away from a stationary light source at absolute speed ua as shown in Figure 9.3. The observer’s relative speed of light decreases and the rules for time dilation compensation (Section 7.15.4) are applied.

Equation set 9.3 gives the result for wisp theory. Although derived in a manner different from special relativity’s, simple manipulation of the final equation shows that it is identical to Einstein’s Doppler equation.
We have assumed that the light source is stationary in wisp space, and derived the result accordingly. However, we will find later that when the source moves through wisp space the result will be the same as for when it was stationary.
Also we will discover that if both source and observer were in motion through wisp space, the result again will be the same as if the source or observer were stationary.

9.2.6 Doppler effect: observer approaching a stationary source
An observer moves towards a stationary light source at absolute speed ua (Figure 9.4).
The moving observer is subject to the effect of time dilation, which causes the relative speed of light to increase – see the rules for time dilation compensation (Section 7.15.4).

Equation set 9.4 shows the frequency recorded by the observer. Once again simple manipulation of the final equation shows that it matches the prediction of special relativity.

9.2.7 Doppler effect: source moving and observer stationary
A source moves towards a stationary observer at speed vs (Figure 9.5).

The observer measures no increase in lights speed – see section 7.2.2 (Wisp relativity’s principle 2 – absolute speeds are constant).
Time dilation affects the moving source, increasing its relative time period, which in turn increases the wavelength of its emitted light. Also during the time interval (delta T’) the source moves towards the emitted wave crest, and releases the next wave closer to the previous one (Figure 9.6), thereby reducing the wavelength of light moving through wisp space.

The stationary observer is unaffected by time dilation and records the received frequency as the absolute speed of light divided by the wavelength (Equation set 9.5).
When the source passes the stationary observer – moving away, we change the speed vs to -vs, and use the same formula.
The Doppler effect results are identical to those predicted by special relativity.

9.3 Doppler effect – general motion : observer and source moving
An observer and light source move through wisp space at absolute speeds ua and vs respectively (Figure 9.7).

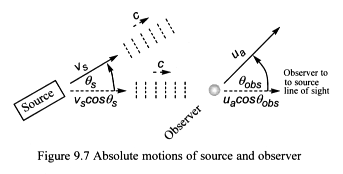
The observer’s relative speed of light increases or decreases, depending on the values of the variables selected.
The absolute speed values chosen for the source and observer can be positive or negative, but they must not exceed the absolute speed of light c.
If we consider the distance between source and observer to be large, then their motions will not affect the angles (theta s) and (theta obs) that they make with the line of sight joining their centres.
We simply input the angle and absolute speed values into Equation set 9.6 to calculate the Doppler effect.

The maximum absolute speed between a source and an observer is twice the speed of light.
If an observer approaches a stationary source at near light speed, the observer will see the source ‘approach’ at a speed greater than that of light. This is an illusion effect caused by time dilation.
Equation set 9.7 shows wisp’s general Doppler equation. Although derived using concepts different to special relativity’s, simple manipulation using a limit process shows that it is identical to special relativity’s Doppler equation.

Wisp’s general Doppler equation calculates the Doppler effect for all observer–source motions through wisp space.
It agrees with special relativity’s predictions in all cases except one – see sections 9.2.1 (Doppler effect: transverse observer motion); 9.2.4 (Testing a moving observer’s transverse Doppler effect); and Appendix A.
The main difference between the two equations is that wisp theory allows for both observer and source to be in separate motions with respect to an absolute reference frame. So its equation has two absolute speed terms and two angles. Whereas special relativity is a limiting case where the observer is at rest in wisp space, and so uses one speed term and one angle.
If we assume that the Earth moves through wisp space at 30,000 m/s, then the relativistic effects on its surface are almost zero, practically undetectable. This explains why special relativity has remained so successful.
However, technology is now available that will allow detection of the Earth’s relativistic effects caused by its motion through wisp space. If results are positive, which I believe they will be, then wisp theory will become a credible alternative to special relativity.