Wisp Unification Theory - 3 Fractals

• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

3

Fractals

Fractals are geometrical figures formed from an identical motif repeating itself on an ever-decreasing scale. Benoit Mandelbrot coined the word fractal in 1975.
Computer programs carrying out simple iteration processes can generate an infinite number of fractal patterns. A small change in the program can change what was a simple pattern into a highly complex one.
Nature is abundant with fractal patterns that are similar to each other on different scales. Many trees grow by making branches that are smaller copies of their basic shape. Fractals appear everywhere, on large and small scales. And I believe that on the smallest scale, the fundamental particles of nature are fractal shapes that form in wisp space.

3.1 Fractal patterns

3.1.1 Cantor dust
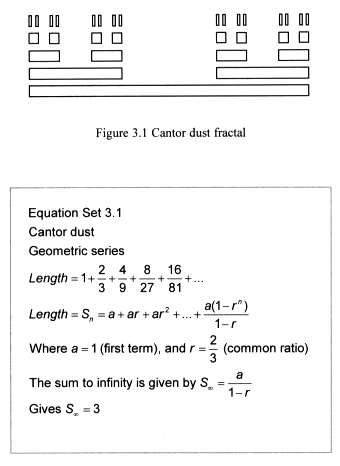
This simple pattern (Figure 3.1) was produced by Georg Cantor around 1870, and is possibly the oldest fractal. It contains patterns that are similar to each other on different scales and is produced by placing lines with their middle thirds removed, above neighbouring lines. After an infinite number of iterations all that remains of the line is a set of dust points of zero length.
If we calculate the total length of all lines we find that we are dealing with a limit process. The lengths of the lines form a geometric series that converge as we take the ‘sum to infinity’. The limit value produced is 3 (Equation set 3.1).

3.1.2 Binary tree
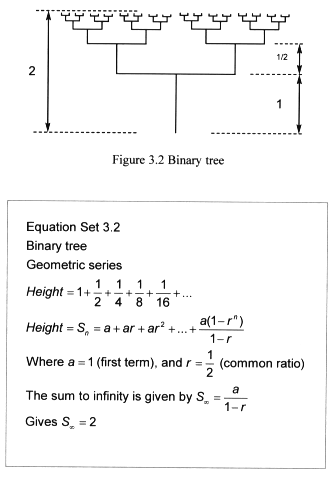
The height of the binary tree is also a limit process (Figure 3.2). At each level the vertical branches split in two, and are halved in size. Each horizontal line is twice the length of the vertical line below it, the vertical lines making the height of the tree form a geometric series that converge as we take the ‘sum to infinity’. The limit value produced is 2 (Equation set 3.2).

3.2 Particle fractals – ‘matter-fractals’
I believe a fractal limit process similarly determines the masses of the fundamental particles. Instead of lines, fractal structures are made up of layers of wisps (weightless one-state particles), held together by strong nuclear binding forces.
Fractals that form the fundamental particles are spherical three-dimensional shapes and the numbers of wisps in them converge to limits, which determine their masses.
It would be extremely difficult to use conventional mathematics to calculate the fractal shapes that form in wisp space. One possible solution would be to use computers running cellular automata programs. I believe this is the way that nature works; it does not have a set of instructions to follow, it just shuffles wisps about and particles pop out.

Home -- About Me -- Reasons why Einstein was wrong -- One-way speed of light experiments -- Hot topic -- Q&A -- ACES - The end of Relativity --
Book Contents -- Introduction -- 1 Matter, Space and Time -- 2 Symmetry -- 3 Fractals -- 4 Wisp Space -- 5 Gravity -- 6 Electromagnetic Force --
7 Wisp & S.R: Fundamentals -- 8 Wisp & S.R: Electrodynamics -- 9 Wisp & S.R: Doppler effect -- 10 Wisp & S.R: Relativistic Mechanics --
11 Big bang -- Appendix A -- Appendix B -- Index A-Z -- Copyright -- Feedback