Wisp Unification Theory - 2 Symmetry
Page last updated 31-Jul-2003

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

2

Symmetry

Wisp theory is essentially a geometrical theory, and an important property of its space is symmetry.


2.1 Symmetry
We tend to associate symmetry with shapes and patterns that stand out from a plain background. Throw a stone into a pond and watch the ripples spread out. They have a high degree of symmetry – circular symmetry. However, the surface of the pond has an even higher degree of symmetry; but because its surface has no interesting features we tend not to notice its symmetry.
Mathematically speaking, symmetry is determined by a process of transformations – rotations, reflections, translations, glide reflections, screw (rotation with translation) – that leave the view of an object unchanged.
Without carrying out any transformations, an equilateral triangle (Figure 2.1) possesses an identity – its shape, its ‘trivial’ symmetry. It has three lines of bisection and it can rotate through 60° or 120° and appear unchanged. It can also be reflected about its lines of bisection, giving it a total of six symmetries.
A sphere has a higher degree of symmetry – spherical symmetry – than say a cube. It can rotate through any angle about a point at its centre, and it look exactly the same; do the same to a cube and it will project different views for different angles. We say that the sphere is spherically symmetric about a point at its centre.
We can determine the degree of symmetry for a cube by rotating it about any of its eight vertices. Including three rotations per vertex and reflections, the cube has 48 symmetries (8 × 3 rotational symmetries, each of which has reflection symmetry).

 

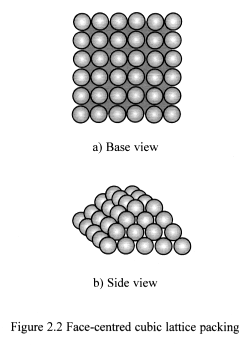
2.2 Face-centred cubic lattice
In 1611 Johannes Kepler conjectured that the face-centred cubic packing is the most economic way of packing spheres in 3-D space – known as the Kepler Conjecture.
It is easy to build a model to demonstrate this (Figure 2.2), but mathematical proof is not so easy to demonstrate.
This method of packing has a high degree of symmetry and forms ‘empty space’ in wisp theory – one-state wisp space. Because this stacking forms parallel planes of wisps, the space is essentially ‘flat space’.


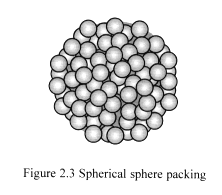
2.3 Spherical sphere packing
If we pack small spheres tightly around a larger central sphere, we obtain a spherical shape similar to that shown in Figure 2.3 (the larger central sphere is hidden from view). However, even though the shape stays roughly spherical there are gaps between the spheres in its outer layers. The reason gaps exist is because the outer layers are curved and the symmetry associated with densely packed flat space gets lost.
Later, I will show that these gaps create spherical tension forces that are responsible for the effects of gravity, where the small spheres represent wisps and the larger central sphere is matter’s ‘zero-state space’.


2.4 Symmetry-breaking
A long circular cylinder is placed upright in a uniformly slow-moving stream, creating a bilateral symmetry flow pattern (Figure 2.4a). As flow speed is increased, vortices that form at the rear of the cylinder begin to break away, alternately shedding from the left and right – vortex shedding.
Increasing flow speed causes the uniform flow associated with bilateral symmetry to become unstable. The pattern breaks forming glide-reflection symmetry flow. This is an example of symmetry-breaking (Figure2.4b).
The surface of a pond has a high degree of symmetry, and by throwing a stone into it, its symmetry breaks, creating circular patterns – ripples.
Many objects that we see around us result from symmetry-breaking processes. They possess symmetries of their own and require separate rules to govern their behaviour.
Later I will show that symmetry-breaking of flat space creates particles. And even through particles have less symmetry than flat space; symmetry-breaking creates objects of complex diversity that are bound by real surfaces.
Symmetry-breaking is responsible for the effects of electric charge. A perfectly formed spherical particle has no electric charge. However, if the inner central ‘zero-state space sphere’ is not perfectly spherical, it will pass its asymmetry on to its outer layers. This causes a clockwise or anticlockwise twist, which is responsible for the positive and negative charge around a particle.


2.5 Antimatter
In 1928 Paul Dirac predicted the existence of antimatter.
Wisp theory considers antimatter to be the mirror image or reflection of matter. Positive charges become negative and clockwise spins become anticlockwise. However, the circular symmetry of a particle still remains circular when reflected, and so gravitational force does not reverse.
It is likely that during the big bang, a state of asymmetry existed in the early universe, causing more matter than antimatter to be created. If the symmetry were perfect at that time, equal amounts of matter and antimatter would have formed, resulting in complete annihilation of both.


2.6 Subatomic particles
In 1962 Murray Gell-Mann and Yuval Ne’eman used symmetry to organise the particles into families. And in 1964 Murray Gell-Mann and George Zweig independently proposed that the hundreds of discovered particles could be explained by combinations of two or three fundamental particles called quarks. (Quarks were named by Gell-Mann from the call of a bartender in James Joyce’s Finnegan’s Wake: ‘three quarks for Muster Mark’.)
Physicists discovered that particles could be grouped into patterns that formed simple geometrical shapes. And new particles were successfully predicted to fill gaps in these patterns.
After a 17 year search, in 1995 Fermi National Accelerator Laboratory (Fermilab), near Chicago, Illinois, announced the discovery of the massive ‘top quark’. The last quark predicted from its symmetry pattern.
It seems highly probable that the underlying cause of this symmetry is due to the fact that the fundamental particles are made from shapes that possess a high degree of symmetry. Wisp theory supports the view that the underlying cause of this symmetry is spherically shaped wisps that form fractal patterns in wisp space.

 

 
Copyright © Kevin Harkess 2002 - 2012. All rights reserved. Harkess Research.