• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

8

Wisp and Special Relativity: Electrodynamics

8.1 Electrodynamics of moving bodies
Inertial reference frames that move through wisp space do so with respect to absolute frames in which the wisps are stationary. And so we cannot simply switch between stationary and moving frames and expect all laws of physics to be the same.
For example, in stationary frame S an electron moves and generates a magnetic field by rotating its electric field pattern in the surrounding wisp space. So we know that the physical effect of pattern rotation does occur in wisp space.
Now consider yourself moving with the electron (frame S’). From a purely relativistic viewpoint, special relativity would argue that because the electron is stationary in frame S’ no magnetic field exists, and any force that results must be purely electrostatic in origin. Indeed, Einstein successfully used this argument in special relativity to explain the Lorentz force law. But here, the two frames differ only by a uniform linear boost – linear velocity translation – and so we cannot simply say that patterns in wisp space have stopped rotating.
However, we can show that relativistic effects in moving frames can make some physical laws behave in ways that are indistinguishable from those in an absolute rest frame.
First we look at the total electromagnetic force F acting on a charge q, with velocity v, moving in electric and magnetic fields E and B, as given by the Lorentz force law

8.2 Force measurements in different frames
We will calculate the electromagnetic force exerted on a particle with charge -q by electrons moving in a wire.
The force will be calculated by stationary and moving observers, first with the wire at rest in absolute wisp space, and then with the wire and observer moving.
Results will show that the magnitude of the force is the same in all reference frames, regardless of whether the wire is moving or stationary in wisp space.
Twentieth-century scientists thought that the properties of ether could not produce equal forces in all frames and so could not support the Lorentz force law. Einstein held this view when he developed special relativity.
But it is not necessary to dismiss the concept of ether to explain the Lorentz force law. As we will now discover, wisp theory shows that the effects of the force are the same in all reference frames.

8.2.1 Electromagnetic force in absolute frame S
A wire at rest in absolute frame S carries a current of electrons, which generate a rotating magnetic field B (Figure 8.1).
The wire has no electrostatic surface charge, because positive ions within the wire neutralize the negative charge on the moving electrons.
A charge -q moves parallel to the wire in the direction of the electron current, and experiences an attractive force F.

Equation set 8.1 shows the equations for calculating the magnitude of the magnetic force. Calculations show that the wire’s magnetic field attracts the moving negative charge towards it.
Since the wire is electrically neutral it experiences no electric force and the force of attraction must be solely magnetic. The measurements made are absolute because the wire and observer are stationary in wisp space, and so the effect of time dilation is absent.

8.2.2 Electromagnetic force in moving frame S’
Now consider the same events as seen by an observer moving with the charged particle (frame S'). In this frame the electrons and the charged particle appear ‘at rest’. So we will hypothesize that the charged particle does not experience any magnetic force, since it is ‘at rest’ (Figure 8.2). (In reality magnetic fields are still present, although to the moving observer in frame S' they would go undetected.)
The purpose of this example is to demonstrate – from wisp theory’s viewpoint – how Einstein came to discover that the electric and magnetic effects are the same thing, but appear different to observers in relative motion. What one observer considers electric another may consider magnetic, and vice versa.
But even though the observer in frame S’ does not detect a magnetic effect, nevertheless it is still present (pattern rotations through wisp space cannot simply be cancelled out through relative concepts), and manifests itself as a change in electric charge. Equation set 8.2 shows the calculations used to measure the magnitude of the relative electric force in frame S’.

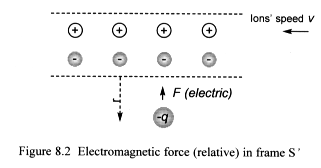
The positive ions are now in ‘motion’ with respect to the ‘stationary’ electrons. In reality the effects of force and jiggle dilations are present, which reduce all negative charges by gamma squared. And the positive ions are really at rest in absolute wisp space and so remain at full strength. This produces the charge strength term (1-1/gamma^2) in the linear charge density equation.
We first expressed the moving observer’s force in absolute terms, and then applied the rules for time dilation compensation, which convert the absolute measurements into relative ones (moving observers’ measurements are always relative).
The calculations show that the wire acquires a net positive electrostatic charge, which acts on the charged particle.
All things being taken into account, we find that a force originating from a magnetic field in one frame compares equally to an electric force in another frame (Equation set 8.3).

Earlier I stated that you cannot simple switch between frames that are absolute and ones that move, and expect there to be no physical changes. In this instance physical changes have taken place – the effectiveness of the negative charges have been reduced by the force and jiggle dilations. However, the moving observer is unaware of any changes as the application of time dilation compensation masks them.
Only by knowing their absolute motions through wisp space can observers determine the true effects of force, jiggle, and time dilations. But even with this knowledge, they will not notice the dilation effects and will measure identical forces in all inertial frames.
However, tests will soon be able to demonstrate the existence of motion through wisp space.
Finally, we calculate the magnitude of the force when both the wire and the observer are moving through wisp space. The dilation effects will be more complex, but the magnitude of the force measured by the observer will be the same as if the wire were stationary.

8.2.3 Electric force on wire moving through wisp space
The wire moves through wisp space at absolute speed Vw. The positive ions, electrons and the negatively charged particle all have their speeds equally increased.
An observer moves with the negative charges (frame S’’). We hypothesize that the effect of the magnetic force in this frame is zero. Equation set 8.4 shows the equations for calculating the magnitude of the electric force.

The effects of force and jiggle dilations apply to all moving charges, but because the positive ions are moving slower than the electrons through wisp space, their dilation effects are smaller.
All charges reduce by (gamma)ea squared because of the effects of force and jiggle dilations. But because the positive ions move slower we must compensate their dilation effects. By dividing their charge by the inverse dilation (gamma”ep squared) we increase their effective charge strength.
We multiply the whole equation by (gamma)ea squared (rules for time dilation compensation).
After time dilation compensation is taken into account, we find that the magnitude of the force of attraction between the moving negatively charged particle and the wire is the same as that found earlier in frames S’ and S.

8.3 Ether re-established
We have proven that all observers measure electromagnetic forces as having the same magnitude in all inertial frames, and so wisp theory proves that the Lorentz force law is valid in an ether medium – wisp space. And so it is not necessary to use Einstein’s concepts of space–time to explain this.
There can be no doubt that the ether is responsible for the effects of the electromagnetic force, and since the force is the same in all frames, Lorentz symmetry - also known as observer Lorentz invariance - is supported in an ether flow.